

To use this method you would have to memorise (or figure out) the following expressions: Solving these equations gives $a=3$, $b=2$ and $c=1$. You can see that for this sequence, $2a=6$, $3a+b=11$ and $a+b+c=6$. In the table below you can see that the second difference is $2a$.Ĭomparing this new table to the original gives another way of figuring out the $n$th term.
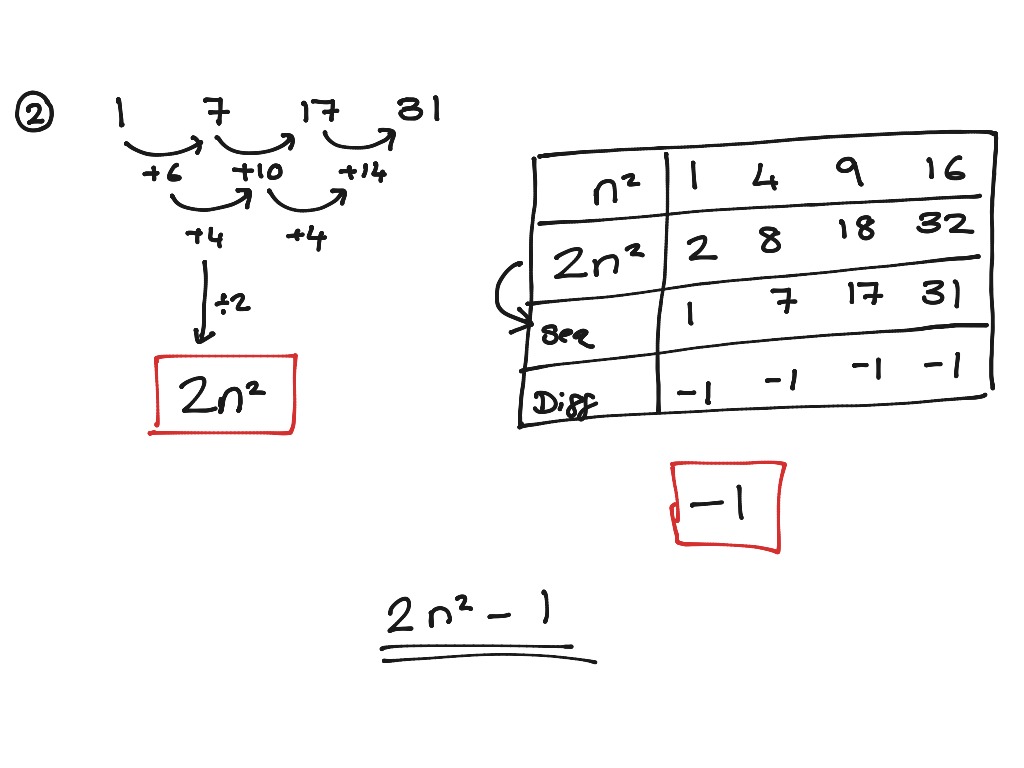
$3n^2+2n+1$īut why is the coefficient of $n^2$ half the second difference? Looking at the general case answers this question. The question marks in the table above can be replaced. Write down the $n$th term of this linear sequence. In this example the linear sequence is 3, 5, 7, … Subtract these numbers from the terms of the given sequence to obtain a linear sequence.Work out the first few terms of the sequence for which the $n$th term is $3n^2$.This is the coefficient of $n^2$ in the required $n$th term, because your teacher says so.The most popular method with teachers seems to be the following: There are several ways to find the $n$th term of a sequence. I hope that the pattern which allows you to work out the next term is clear. The second difference is found in a similar way. The first differences are found by selecting each term, after the first, and subtracting the previous term. In the table below the “working out” has been added below. If the first four terms of a quadratic sequence are 6, 17, 34, and 57, find the next term and the $n$th term. I’m going to focus on the second of these points. Given a sequence, work out the next few terms or figure out the $n$thterm.Given the expression for the $n$th term of a sequence, work out the first few terms, or the 20th term, or any given term.In their wisdom, the people who decide what mathematics you have to learn and what you will be tested on have decided that you need to be able to do at least the following things: … so, if you know the values of $a$, $b$ and $c$ you can work any term of the sequence. The third term is $a \times 3^2+b\times 3+c=9a+3b+c$.The second term is $a \times 2^2 +b \times 2 + c = 4a+2b+c$.The first term is $a\times 1^2 +b \times 1 + c = a+b+c$.The constants $b$ and/or $c$ might be zero but $a$ definitely isn’t. This is a guest post from Mark Ritchings, a maths tutor in Bury.Ī quadratic sequence is a sequence for which the $n$th term is $an^2+bn+c$.


 0 kommentar(er)
0 kommentar(er)
